공개키 알고리즘인 RSA 알고리즘에 대해 알아보자
Public key
- 키를 2개 사용한다
- public key (공개)
- private key (비공개)
- 비대칭 알고리즘이다.
- 활용
- 서명
- A의 비밀키로 암호화 한 메시지를 공개키를 가진 B가 복호화를 하면 A의 메시지인 것을 알 수 있다.
- 메시지 암호화 및 복호화
- 메시지를 암호화 및 복호화하여 통신을 위해 사용할 수 있지만 대칭키 알고리즘 방식보다 느리므로 잘 안 쓴다.
- 키 분배
- 대칭키 알고리즘의 key를 분배하는 데 사용한다.
- 서명
공개키 암호 알고리즘이 가져야 하는 기본적인 특성
- 알고리즘, 공개 키만 가지고 복호화 키를 찾는 것은 계산적으로 불가능
- 키만 있으면 암복호화가 쉬워야 한다.
- 하나의 key로 암호화했으면 다른 key로 복호화한다.
RSA 알고리즘
- RSA알고리즘은 큰 두 소수의 곱 N이 있을 때 두 소수를 찾기 힘들다는 생각에서 만들어졌다.
- Φ(n) (오일러 피 함수)는 양의 정수 n에 대해, n과 서로소인 1부터 n가지의 양의 정수의 개수를 나타낸다.
- Φ(n)이 n = p * q(p , q는 소수) 라면 (p-1) * (q-1)을 계산을 통해 빠르게 구할 수 있다.
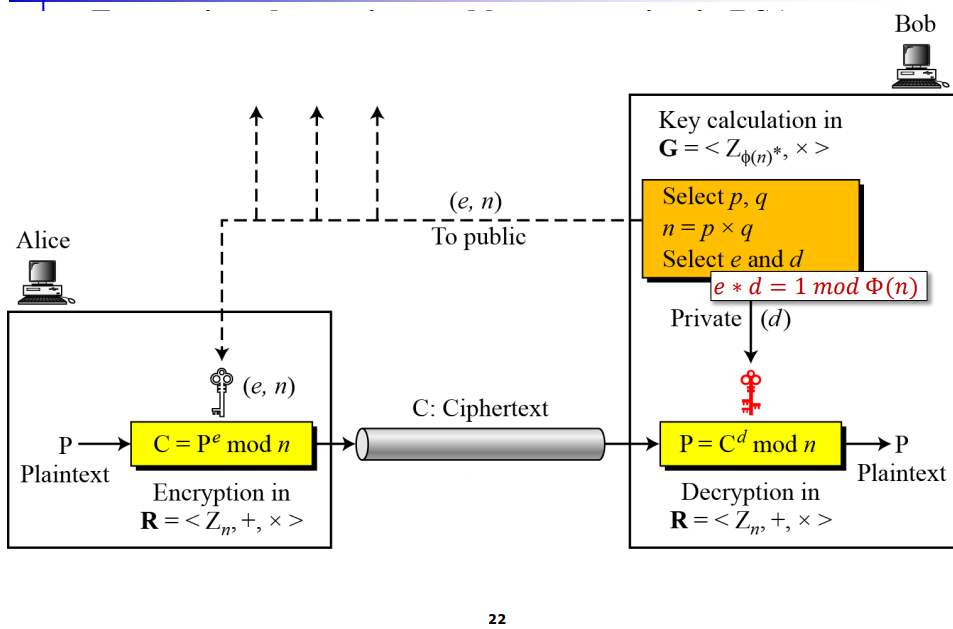
- 밥은 큰 두 소수 p, q를 이용해 N을 생성한다.
- mod Φ(n) 연산에서 n과 서로소인 e를 선택한 후 e와 곱셈연산에서 역원 관계인 d를 계산한다.
- e * d = 1 mod Φ(n)
- n과 e가 서로소 이어야 하는 이유는 e로 n을 나누었을 때 나머지가 0이 되면 안 되기 때문이다.
- N과 공개키인 e를 공개한다.
- Alice는 평문을 e승한 것을 mod n연산을 통해 암호문 C를 구한 후 밥에게 전송한다.
- 밥은 C를 비밀키인 d로 C^d를 한 후 mod n연산을 취해 평문 P를 얻을 수 있다.
- P^e = C가 되고 이를 받은 밥이 P^e (C)에 d승을 하면 P^e^d mod n에서 e*d = 1이므로 P가 된다.
- 오일러 정리에 의해
- a ^ Φ(n) ≡ 1 mod n (a와 n은 서로소)
- e*d = k* Φ(n) + 1로 표현가능하다. (k는 임의의 몫)
- e * d = p*q + 1
- 공격자는 공개키인 e와 N을 알더라도 Φ(n)은 계산이 매우 어렵기 때문에 비밀키인 d를 계산하지 못한다.
- 하지만 밥은 p, q를 알고 있으므로 Φ(n)을 (p-1) * (q-1)을 통해 매우 간단하게 계산을 할 수 있다.
간단한 예시
- 밥이 두 소수 p = 17, q = 11을 선택한다.
- n = p * q = 187이 된다.
- Φ(n) = 16 * 10 = 160이 된다.
- 160과 서로소인 e를 선택한다. e = 7을 선택하자
- e * d = 1 mod 160인 d는 23이 된다.
- 엘리스가 전송할 메시지를 M = 88이라고 하자
- 88 ^ 7 mod 187 = 11이 된다.
- 11이 암호문이므로 이를 밥에게 전송
- 밥은 11을 받은 후 비밀키인 23을 이용해 11^23 mod 187 계산을 통해 88을 얻을 수 있다.
'보안' 카테고리의 다른 글
| [Wireless Security] 무선 보안 (IEEE 802.11 Wireless LAN) (0) | 2024.12.16 |
|---|---|
| Firewall (1) | 2024.12.13 |
| [IDS] 침입 탐시 시스템 (0) | 2024.12.09 |
| [이메일 보안] PGP (0) | 2024.12.01 |
| 세션 하이제킹 (0) | 2024.10.18 |