[B트리] 속성과 삽입

출처 : https://www.youtube.com/watch?v=bqkcoSm_rCs

B tree

아래와 같이 이진트리에서 확장해 자녀에 3개의 값을 저장하고 싶어 사용한 트리이다. 

자녀를 최대 몇 개까지 가질 수 있게 할 것이냐가 중요하다.

파라미터

M = 각 노드의 최대 자녀 노두 수

M-1 = 각 노도의 최대 key 수

[M/2] = 각 노트의 최소 자녀 수 (루트랑 리프노드는 제외한다.)

[M/2] - 1 = 각 노드의 최소 key 수

 

 

특징

internal 노드의 key 수가 x라면 자녀 노드의 수는 언제나 x+1개이다.

그러므로 아래와 같은 경우는 존재하지 못한다.

즉 노드는 최소 하나의 key를 가지기 때문에, 몇 차 b tree인지 상관없이 최소 두 개의 자녀는 가진다.

M이 정해지면 root를 제외하고는 최소 [M/2] 개의 자녀노드를 가진다.

 

데이터의 삽입

추가는 항상 leaf에 추가된다.

key들은 오름차순으로 저장이 되어야 한다.

노드가 넘치면 가운데 key를 기준으로 좌우 key를 분할하고, 가운데 key는 승진한다.

정렬된 형태로 추가를 한다.

추가가 되는 과정에서 모든 leaf노드는 같은 레벨에 있다.

 

1 삽입 

 

15 삽입

2 삽입

오름 차순으로 삽입을 해야 하기 때문에 2를 중간에 삽입 -> 노드가 3개로 넘쳐 났기 때문에 분할을 해주어야 한다.

 

1과 15를 분할한 뒤 2를 새로운 루트 노드로 승진한다.

30 삽입

30을 추가하면 또 분할을 해야 한다.

20 추가

 

정렬된 형태로 저장 -> 분할 필요

30 승진 후 에도 부모에서 또 분할이 필요하다.

최종 분할 후 

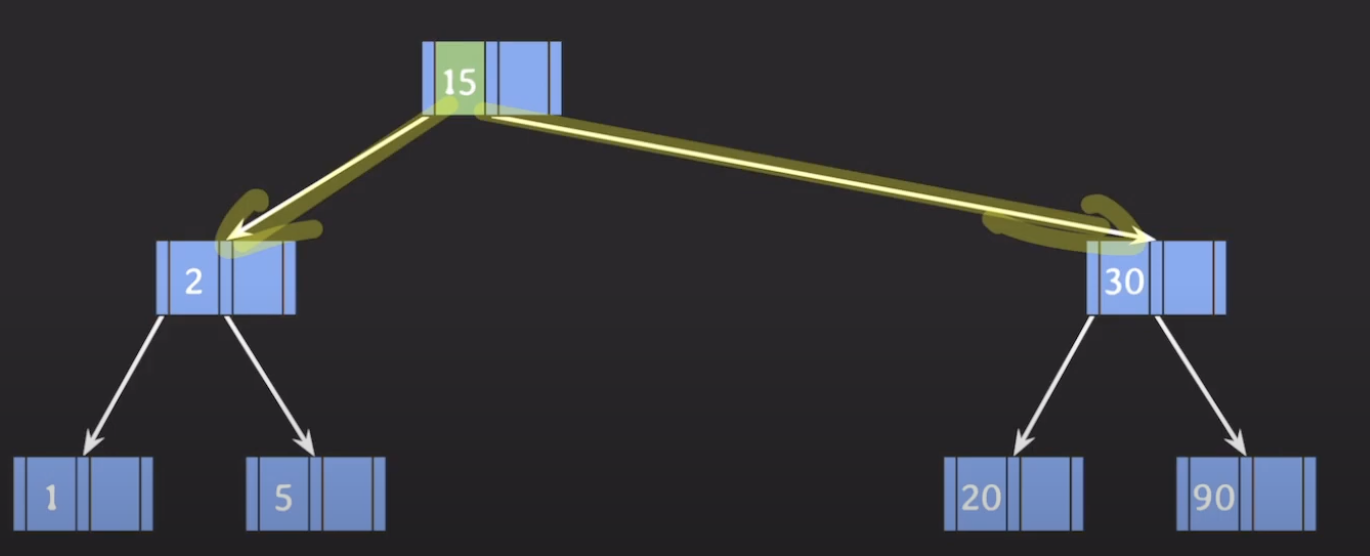
데이터 삭제

삭제도 항상 leaf노드에서 한다.

삭제 후 최소 key 수보다 적어 젔다면, 항상 재조정을 해야 한다.

 

1. key 수가 여유 있는 형제의 지원을 받는다.
2. 1번이 불가능하다면, 부모의 지원을 받고 형제와 합친다.
3. 2번 후 부모가 문제가 있다면, 거기서 다시 재조정한다.

동생의 도움

형제 중 먼저 동생의 도움을 받는다.

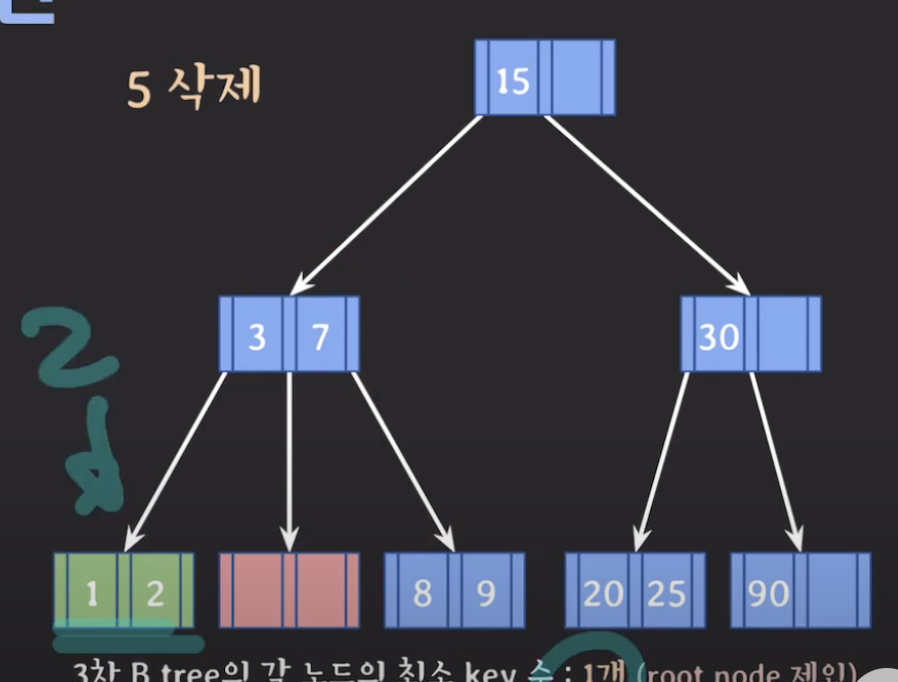
b트리의 특성을 만족하면서 옮겨야 하기 때문에 아래와 같이 부모를 한 칸 내리고 동생을 부모로 올린다.

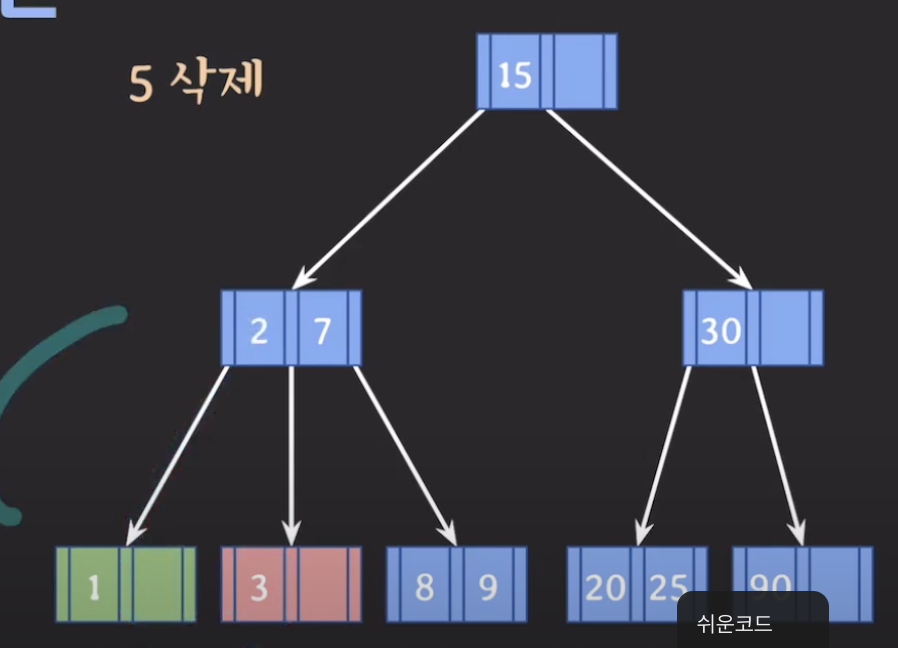
형의 도움
아래는 동생의 도움을 못 받으므로 형한테 도움을 받는다.

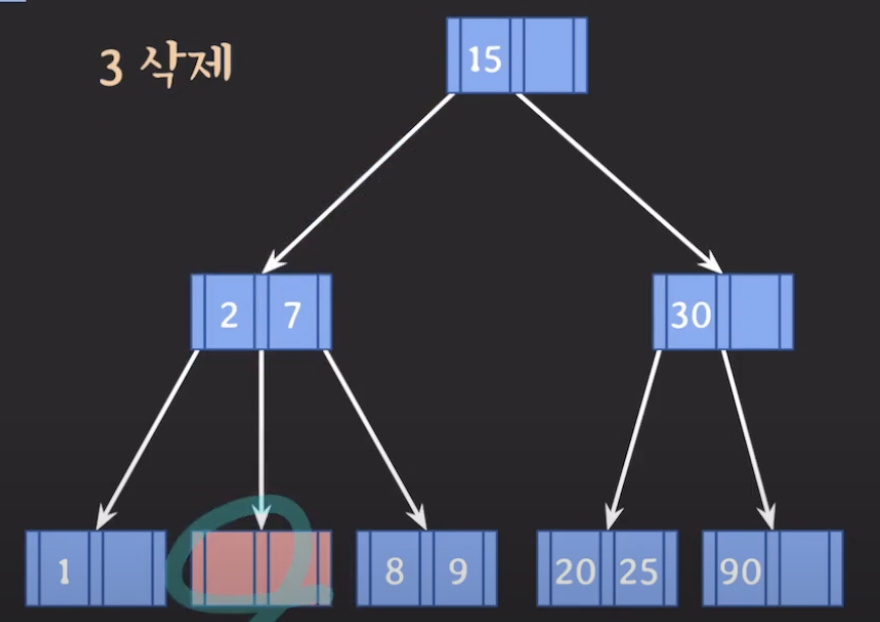
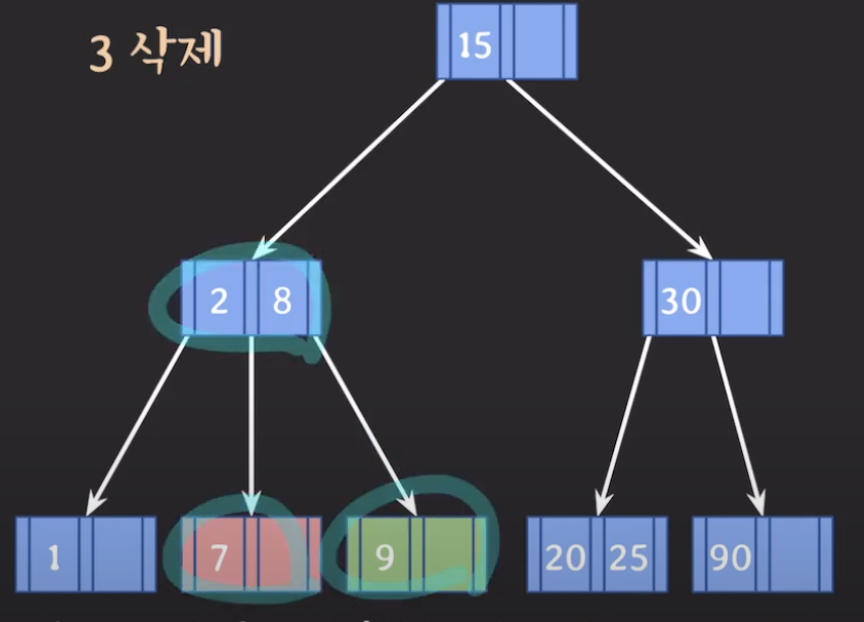
부모의 도움

형제 도움을 받지 못하는 경우

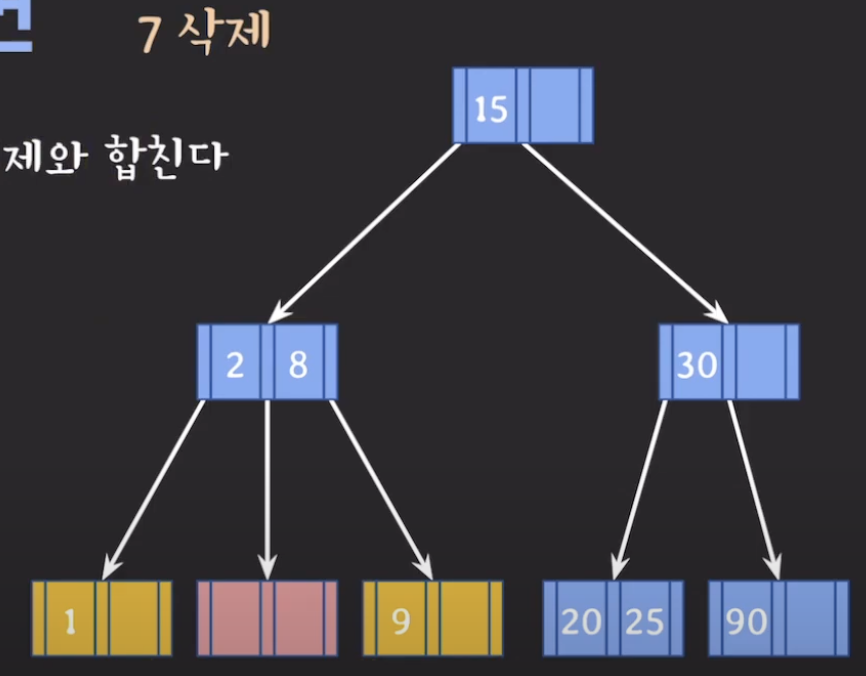
부모에게 도움을 받는다. 자신을 동생이랑 합친다. 

 

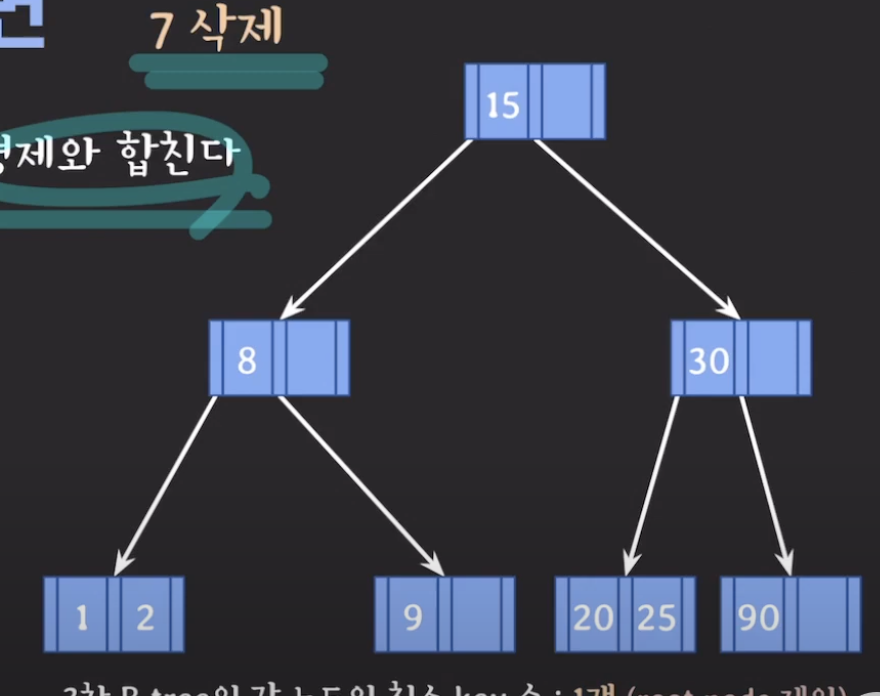
부모도 도움을 받는 경우

아래와 같은 경우에는 부모의 도움을 받아 형과 합친다.

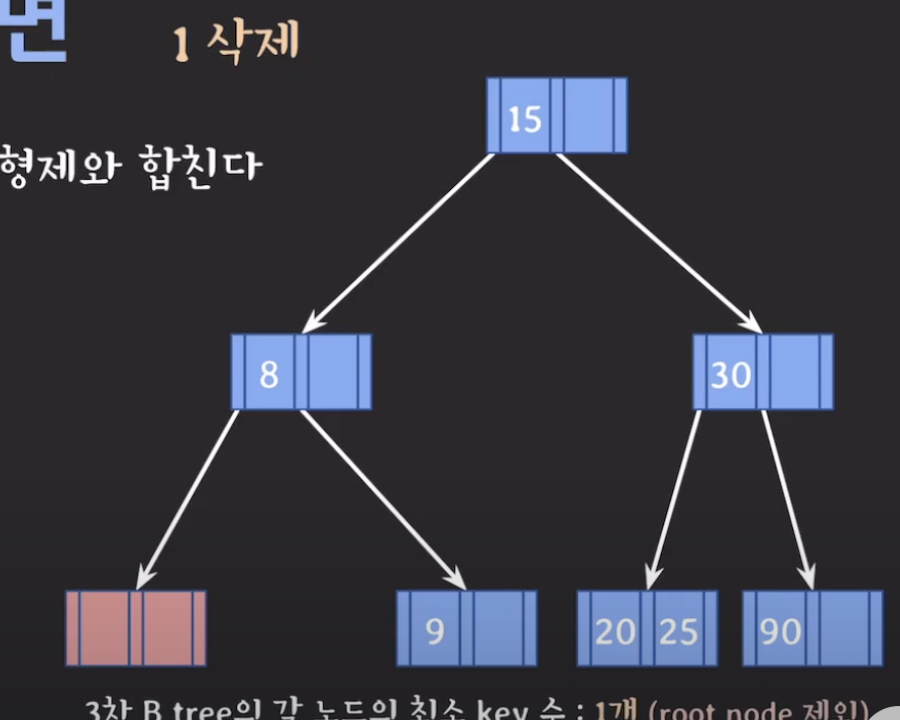
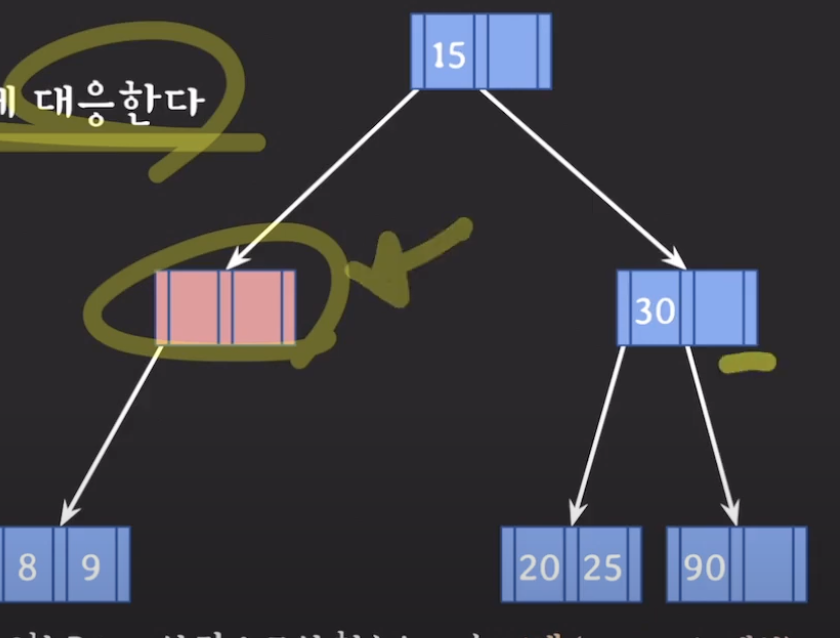
부모의 도움을 받아 합친다. 포인터도 다 따라옴 그 후 빈 것은 제거한다.

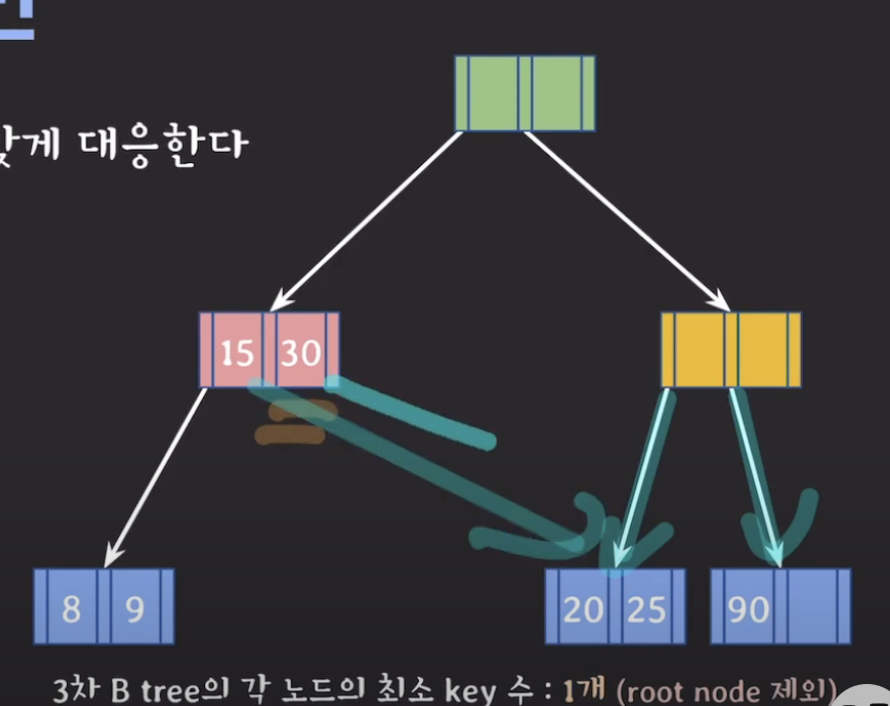
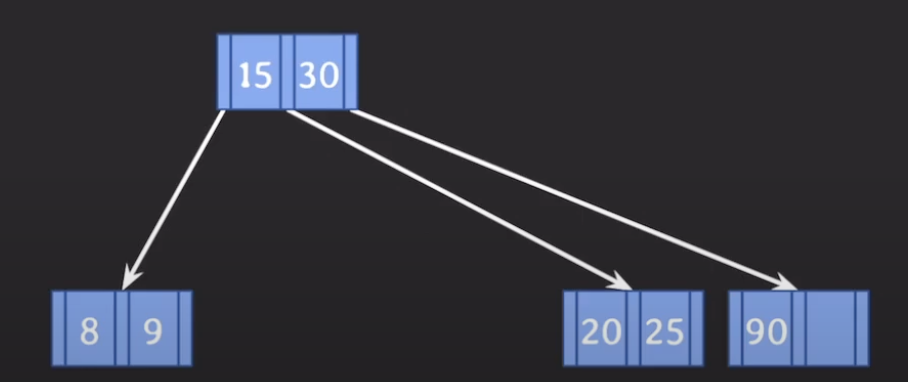
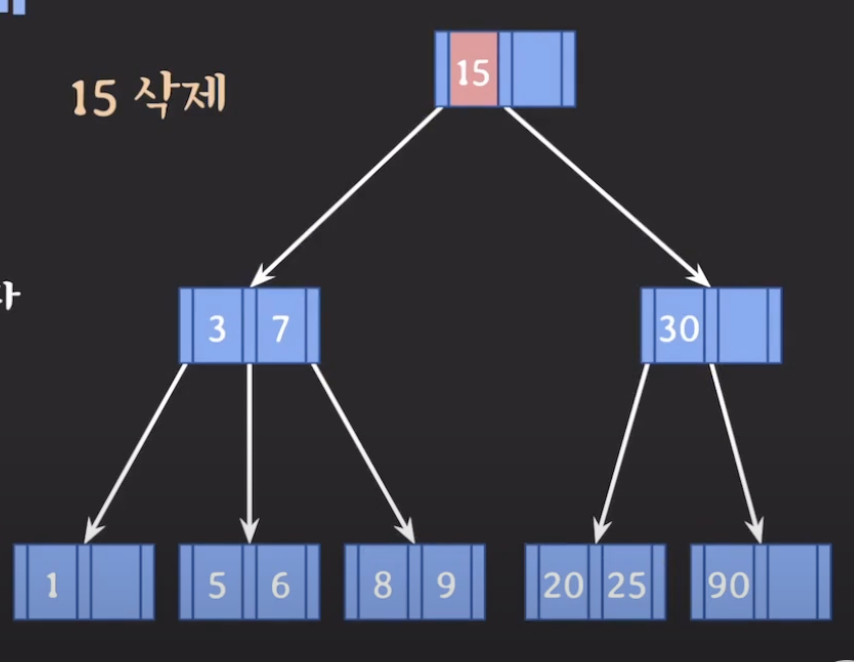
internal node 삭제

internal node와 leaf노드의 위치를 바꿔준 후 삭제한다.

리프 노드 중 선임자, 후임자와 바꾸어 준다.

선임자 (나보다 작은 데이터 중 가장 큰 값), 후임자(나보다 큰 값들 중 가장 작은 값)